ICACT20240330 Slide.20
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
Thank you!
|
|
ICACT20240330 Slide.19
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
Here are the references.
|
|
ICACT20240330 Slide.18
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
Lastly, we have implemented and evaluated the |Y> state distillation processes for logical S gate. We validated the distillation circuit by implementing two methods based on the lattice surgery model and evaluating the cost of each method. As a next step, we will implement and evaluate the |A> state distillation processes for the logical T gate.
|
|
ICACT20240330 Slide.17
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
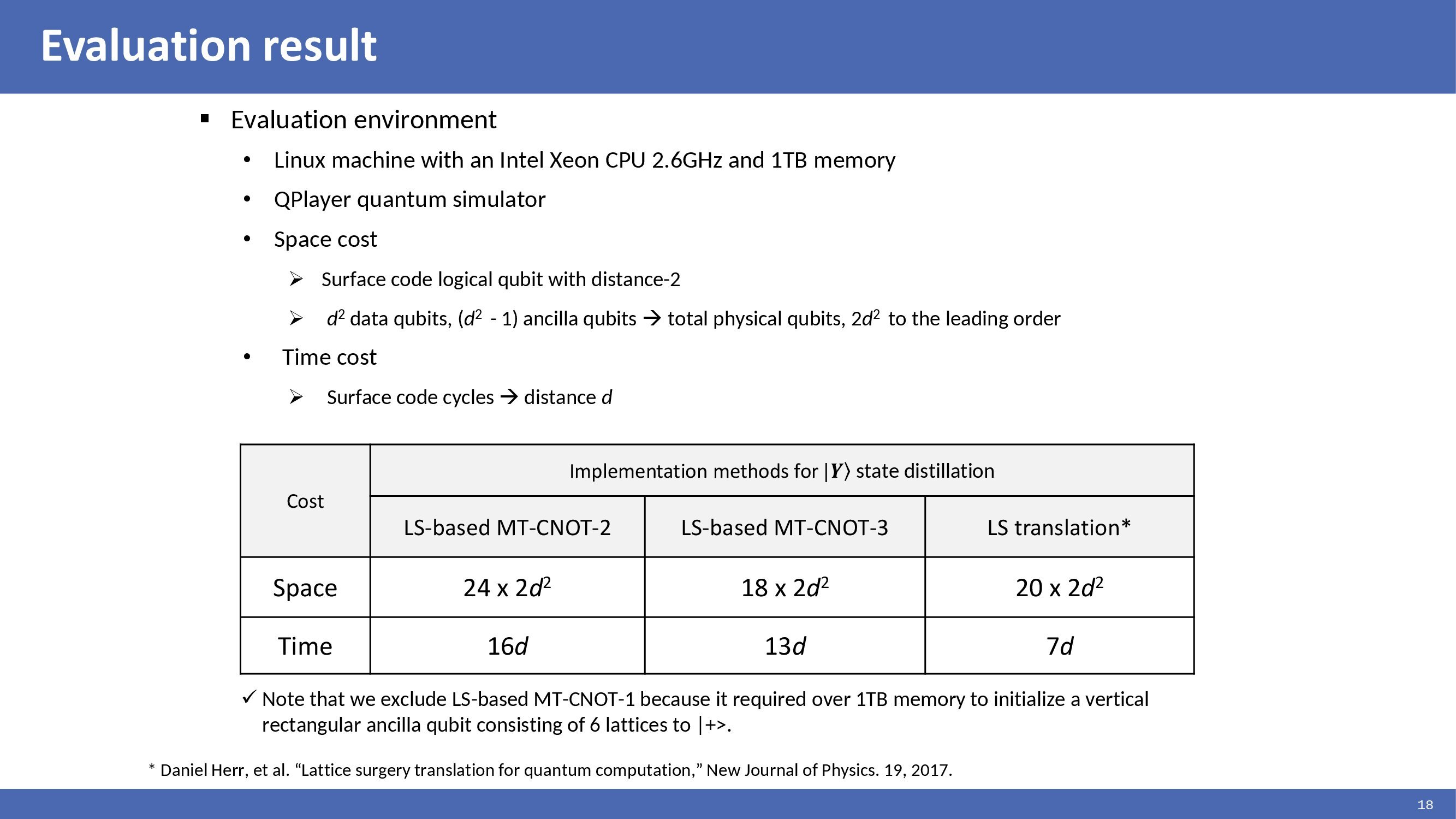We have implemented and evaluated this environment. We used a QPlayer quantum simulator. The metrics are space and time costs. The space cost can be given regarding the number of physical qubits. We used surface code logical qubits with a distance of 2, so the space cost is 2d squared. The evaluation results show that the Y-state distillation circuit can be implemented using lattice math. Daniel's method can implement the distillation circuit at a lower cost. However, Daniel's method requires considering the layout structure to achieve optimal results. However, the distillation circuit can also be implemented in a regular checkerboard logic qubit structure with fewer qubits.
|
|
ICACT20240330 Slide.16
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
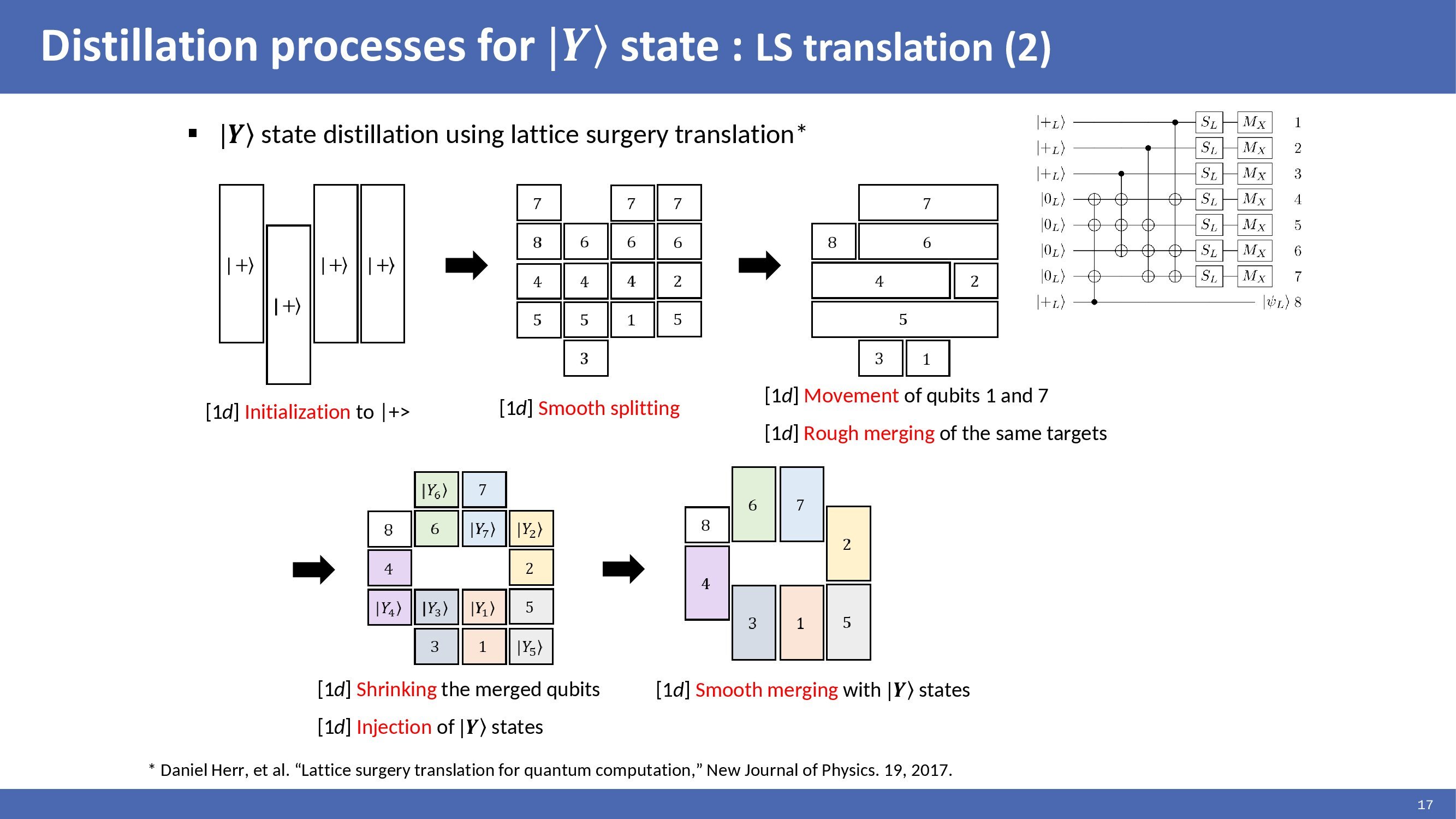|Y> state distillation circuit consisting of multi-target CNOTs can be translated to lattice surgery as presented by Daniel and implemented as shown in the figures. In the figures, each rectangular corresponds to a multi-target CNOT. Each rectangular is split, and the identical target qubits are merged to perform CNOT operations. This method reduced the time cost by translating multi-target CNOTs to be suitable for lattice surgery.
|
|
ICACT20240330 Slide.15
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
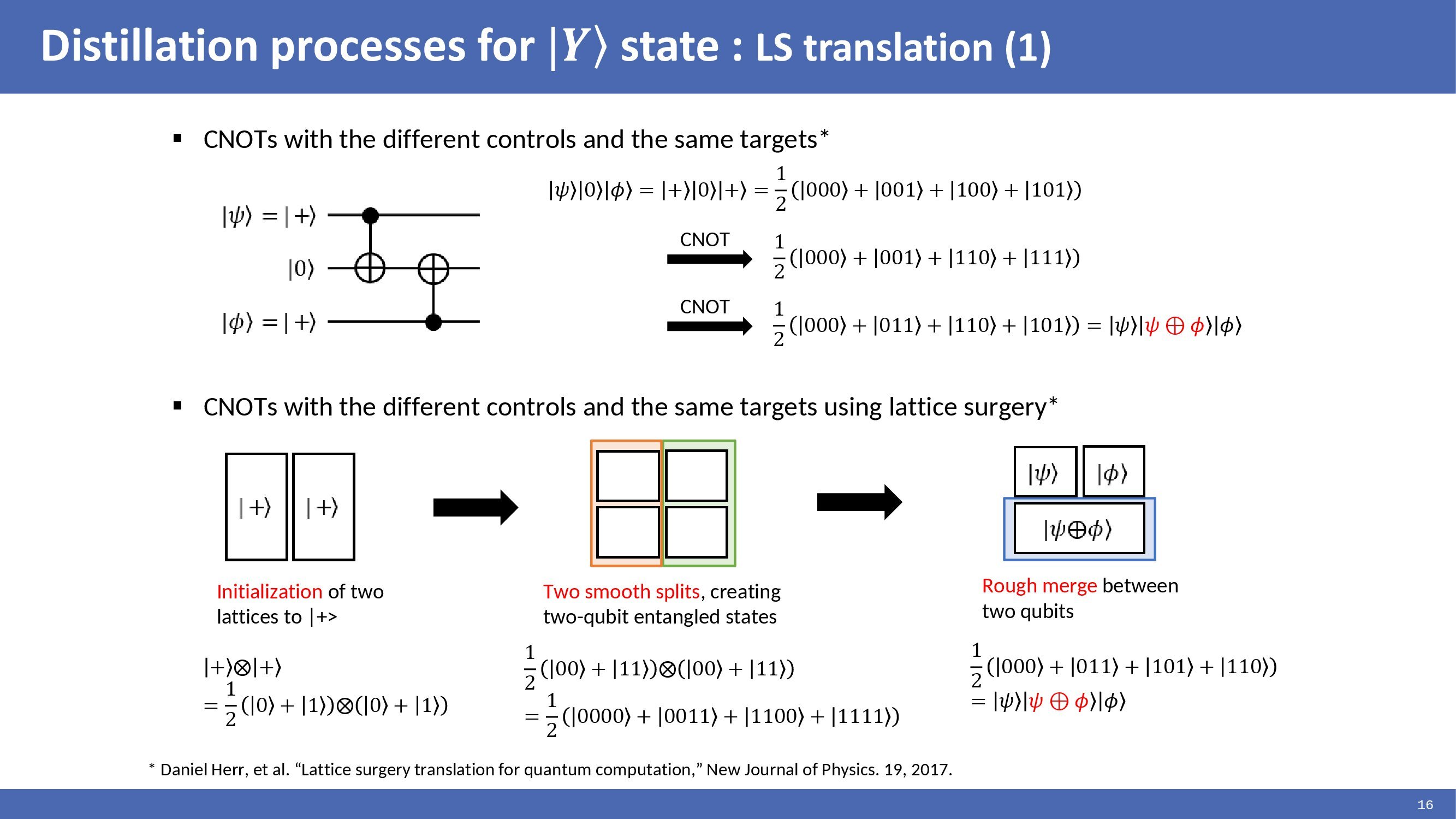Daniel's paper presented that the lattice surgery method can implement CNOT operations with different controls and the same targets. This example show that a circuit with two CNOTs can be translated to lattice surgery operations and get the same result. This example can be extended to multi-target CNOTs, as shown in |Y> state distillation circuit.
|
|
ICACT20240330 Slide.14
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
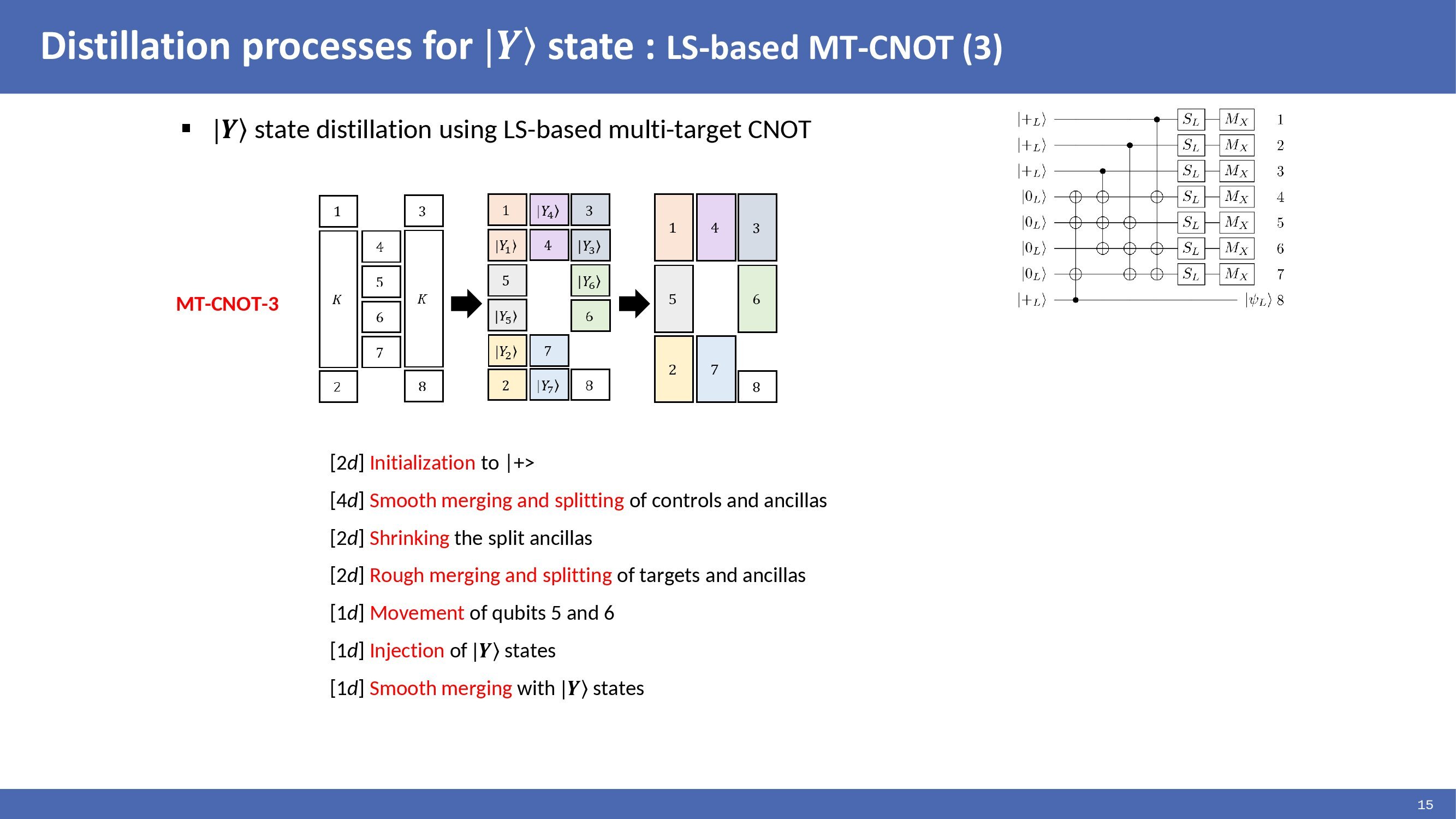Here, we have implemented |Y> state distillation circuit in a logical qubit architecture with 18 logical qubits. The time cost of performing multi-target CNOTs and logical S gates are as follows.
|
|
ICACT20240330 Slide.13
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
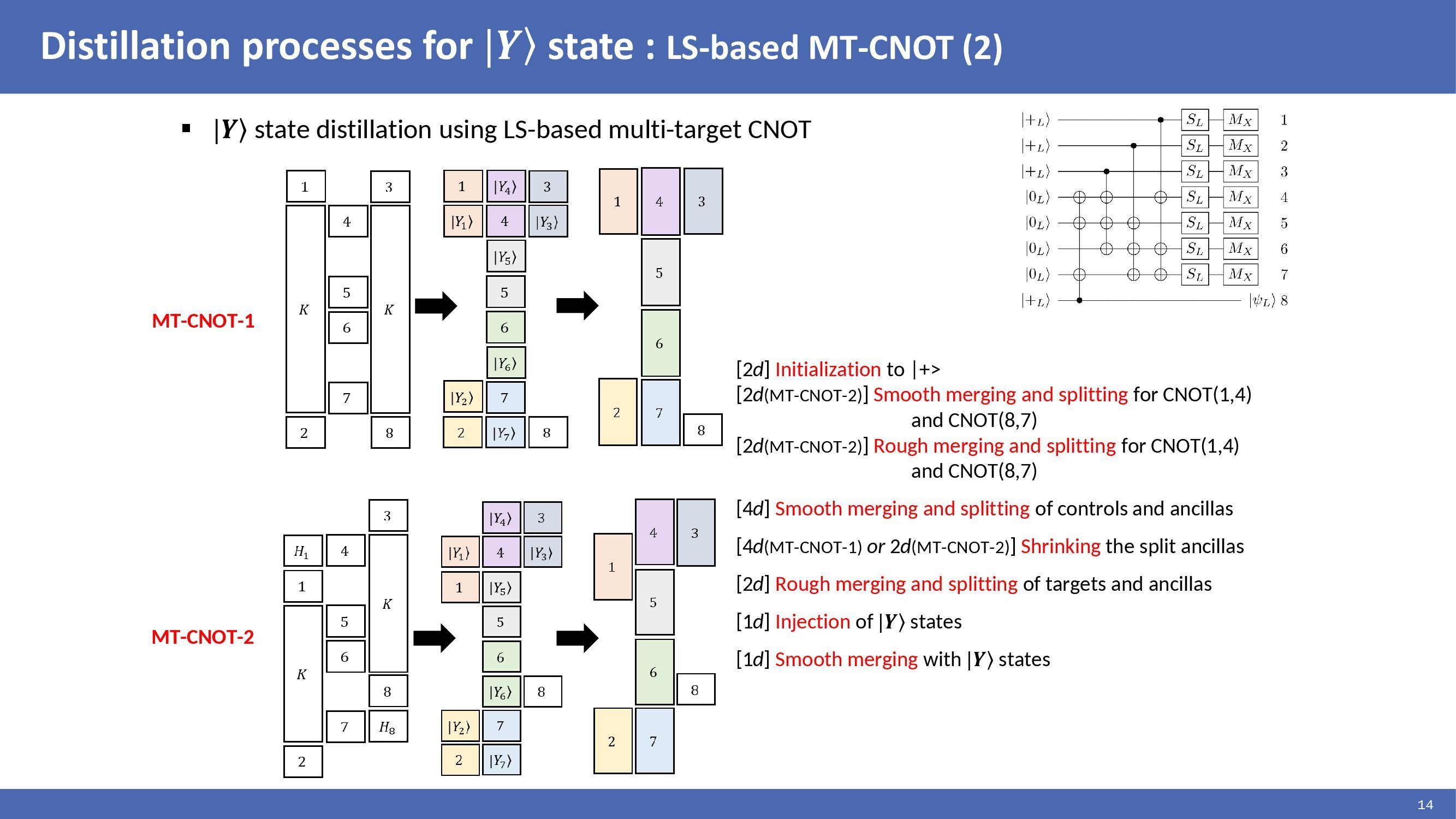|Y> state distillation circuit using lattice surgery multi-target CNOTs was implemented and evaluated in a logical qubit architecture consisting of 24 logical qubits for two different qubit arrangements. Lattice surgery multi-target CNOTs and logical S gates are performed on each arrangement. In the second arrangement, the first and fourth multi-target CNOTs are split into two CNOTs because it takes over 1TB of memory to initialize a rectangular ancilla qubit of six lattices to |+>. These operations are performed for |Y> state distillation process. The time cost is given for logical operations by d rounds ESM cycle of surface code logical qubit.
|
|
ICACT20240330 Slide.12
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
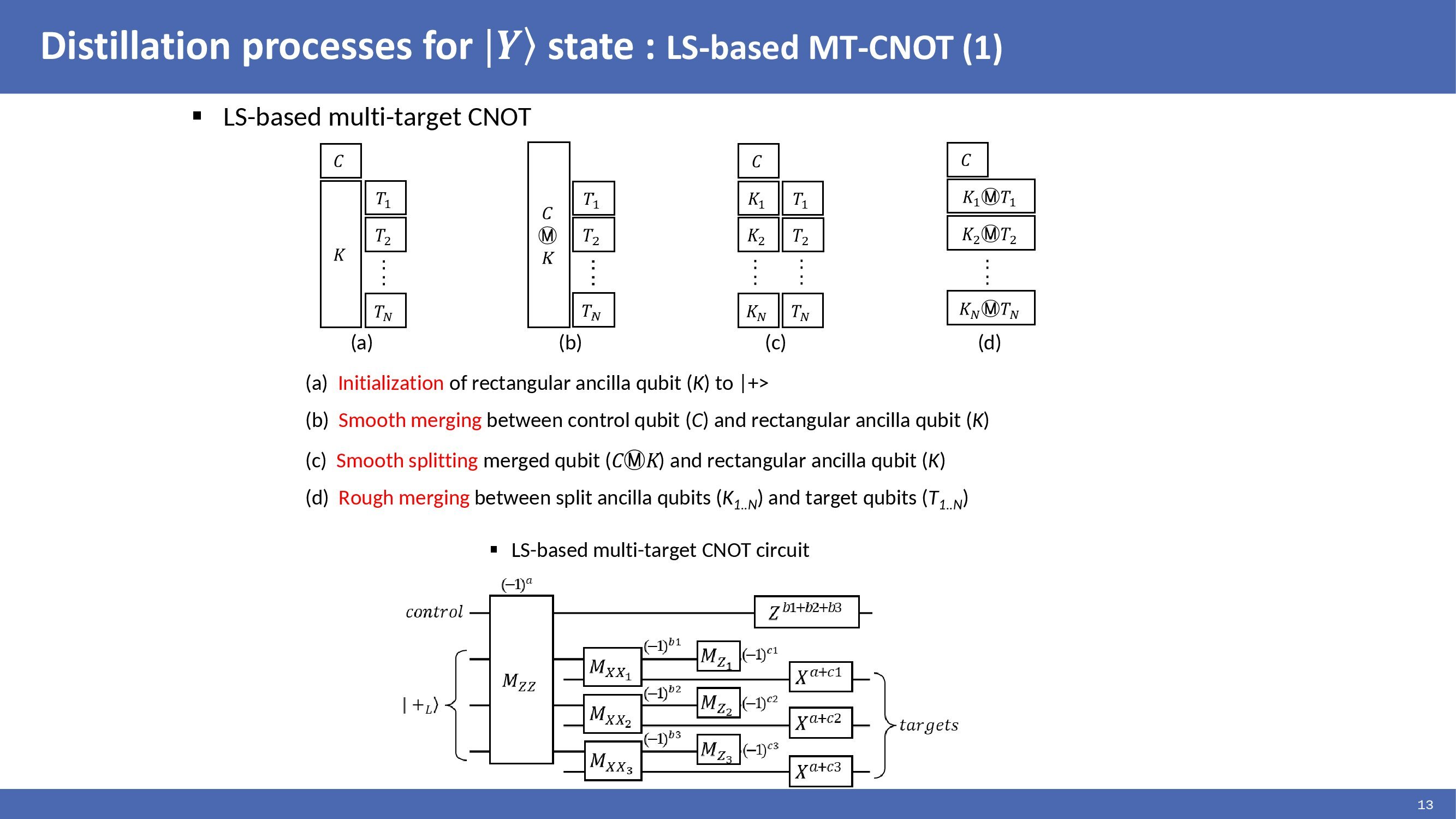Lattice surgery-based multi-target CNOT can be depicted as follows:
Firstly, the rectangular ancilla qubit is initialized to |+>. Control qubit is smoothly merged with rectangular ancilla qubit. After that, the merged qubit and rectangular ancilla qubit are smoothly split. Finally, split ancilla qubits and target qubits are roughly merged. The figure represents a lattice surgery-based multi-target CNOT circuit.
|
|
ICACT20240330 Slide.11
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
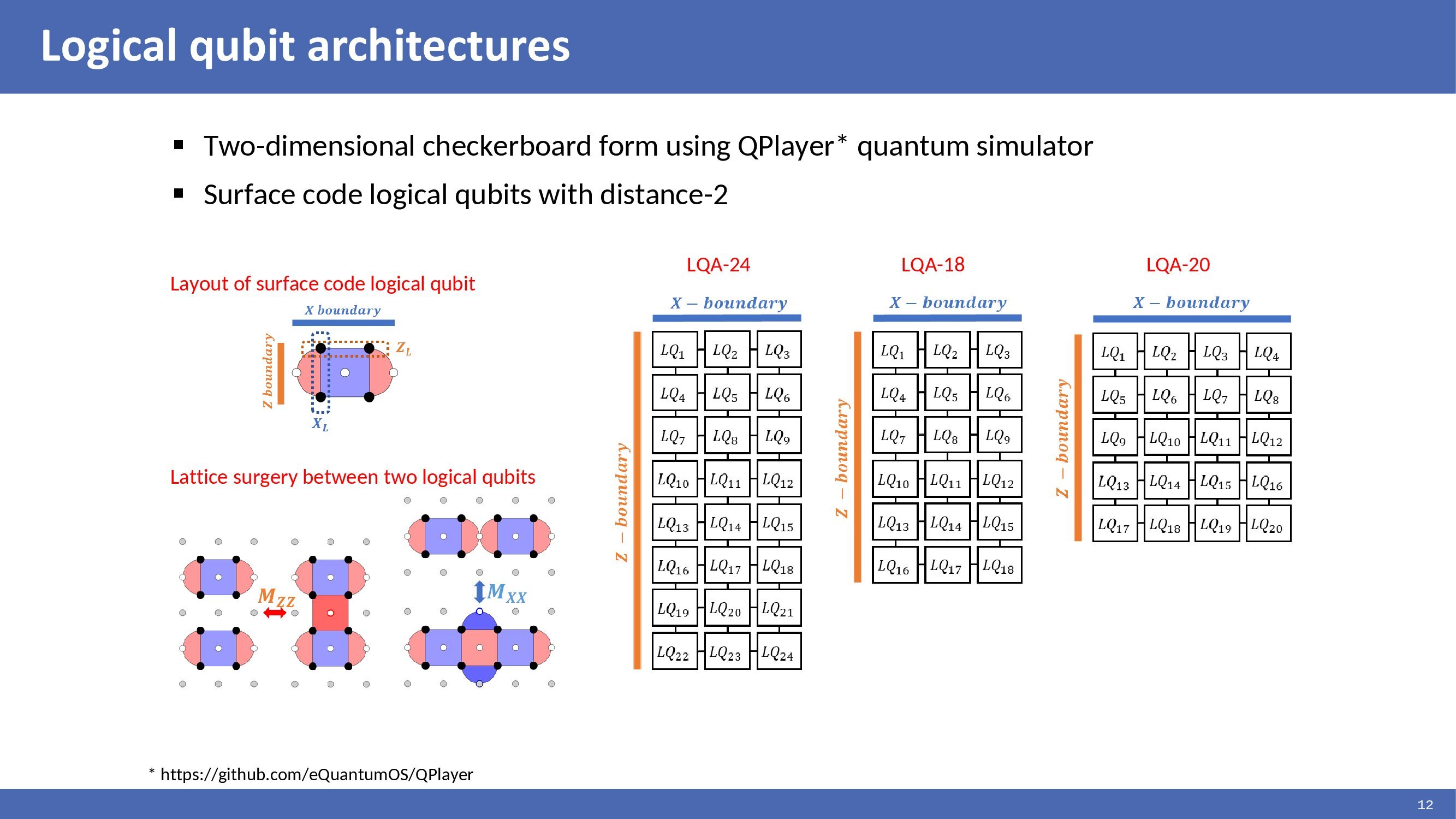We have constructed a two-dimensional checkerboard form of logical qubit architecture using the QPlayer quantum simulator to implement and evaluate the distillation processes. Each logical qubit is encoded as rotated surface codes with distance 2. It requires seven physical qubits to encode a logical qubit. Figures show the layout of the surface code logical qubits and the lattice surgery method between two logical qubits. The figures show that the distillation processes were implemented in a logical qubit architecture of 24, 18, and 20 qubits.
|
|
ICACT20240330 Slide.10
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
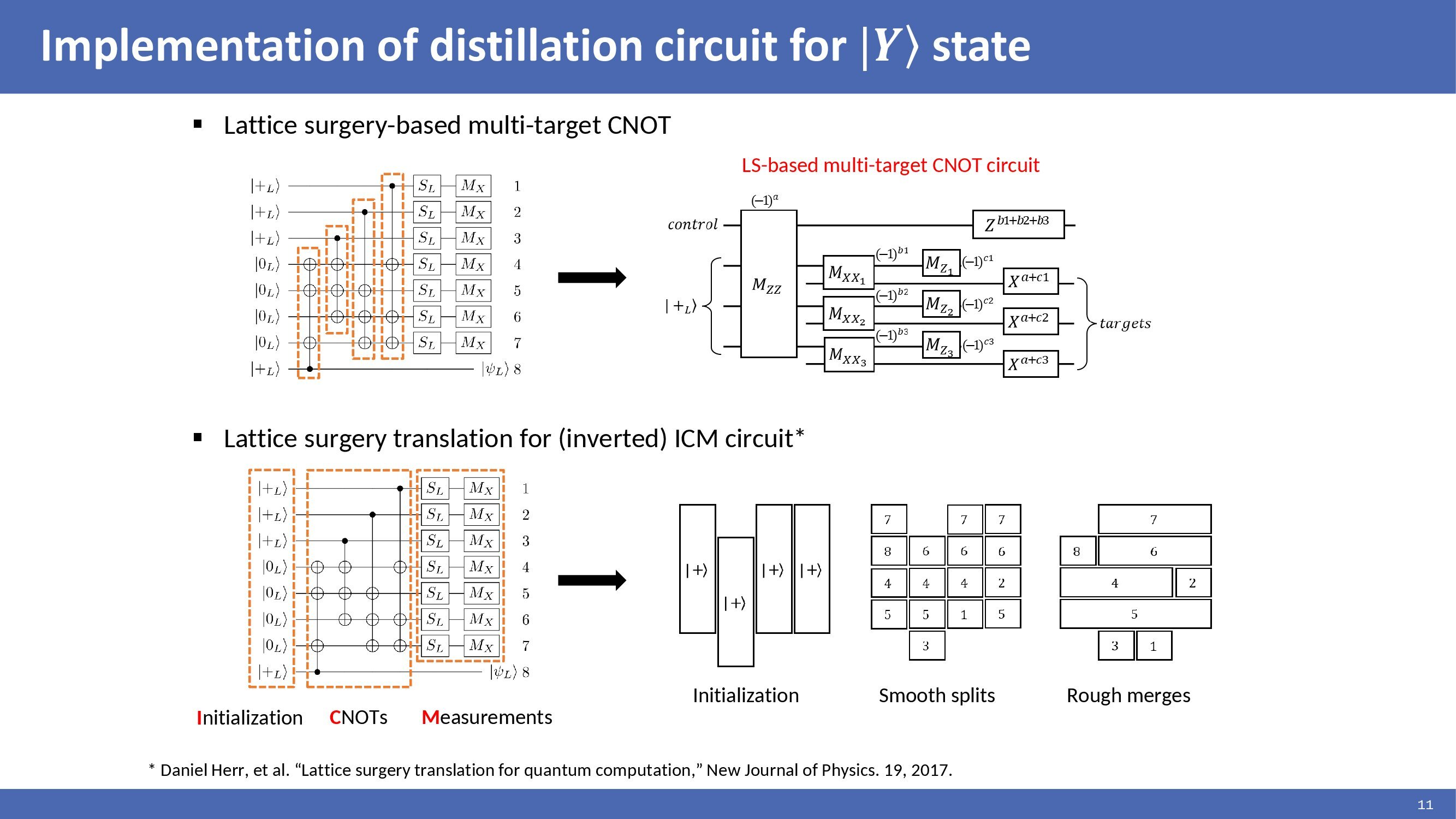In this work, we have implemented a distillation circuit for the |Y> state with two methods. First, we have implemented a distillation process with lattice surgery-based multi-target CNOTs. Second, we have implemented a lattice surgery translation-based distillation process presented by Daniel Herr. He has presented that the circuit of ICM form is easy to translate to the lattice surgery model. The ICM circuit consists of Initialization, CNOT, and measurement. The distillation circuit has an inverted ICM format. And so it can be implemented using lattice surgery.
|
|
ICACT20240330 Slide.09
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
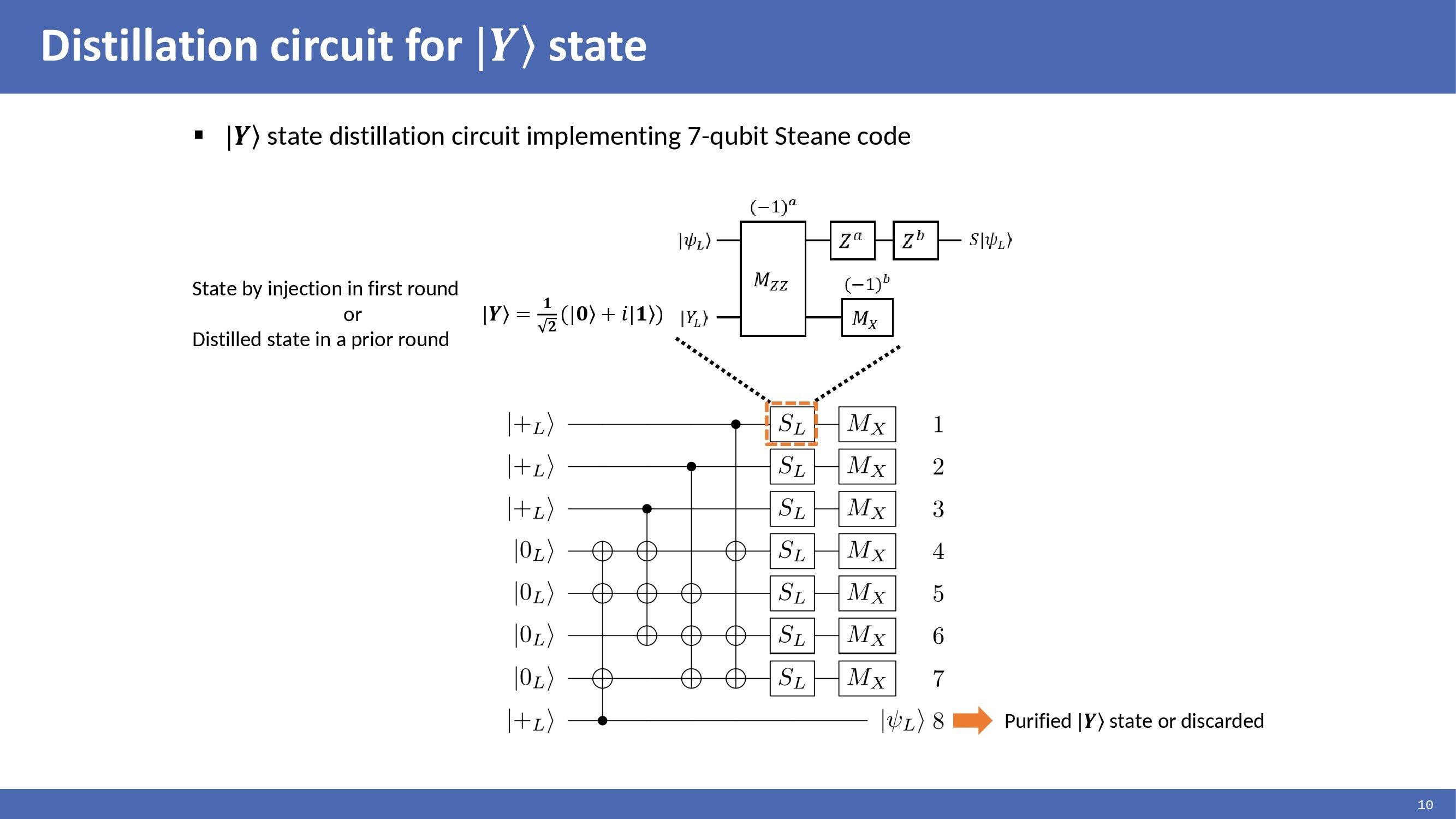The distillation circuit for |Y> state can be implemented using the 7-qubit Steane code. The 7-qubit Steane is one of the quantum error correction codes. This circuit consists of initialization of |0> and |+>, multi-target CNOTs, logical S gate teleportation, and X-basis measurements. In this circuit, seven qubits are encoded in Steane code and entangled with qubit 8 using the multi-target CNOTs. After that, seven encoded qubits are each rotated with an S gate using |Y> state. The |Y> state used is either the injected state in the first round or the state distilled in a prior round. The output state on qubit 8 is interpreted by evaluating the X-basis measurement outcomes of the seven qubits and eigenvalues of the Steane code X stabilizers. If the two conditions are satisfied, the output is considered purified |Y> state. Otherwise, the state is discarded, and the subsequent distillation rounds are performed.
|
|
ICACT20240330 Slide.08
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
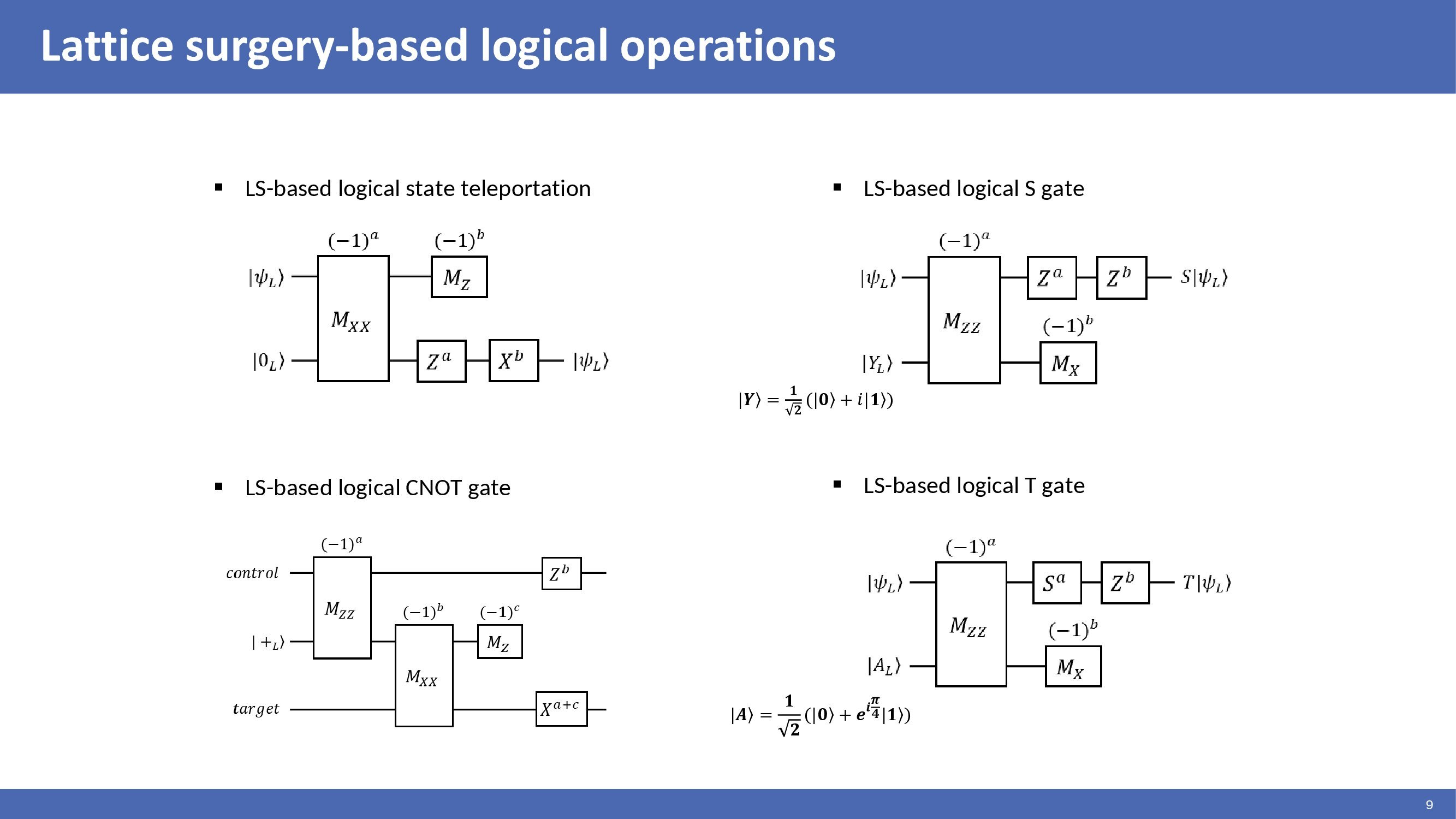These circuits show lattice surgery-based logical operations. The logical qubit state can be teleported to the other qubit by logical joint measurement Mxx. Logical CNOT between two logical qubits can be performed through an ancilla qubit using logical joint measurements Mzz and Mxx. Logical S and T gates can be performed by gate teleportation using magic states |Y> and |A>. The Pauli corrections are performed post-operations in these circuits depending on the measurement outcomes.
|
|
ICACT20240330 Slide.07
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
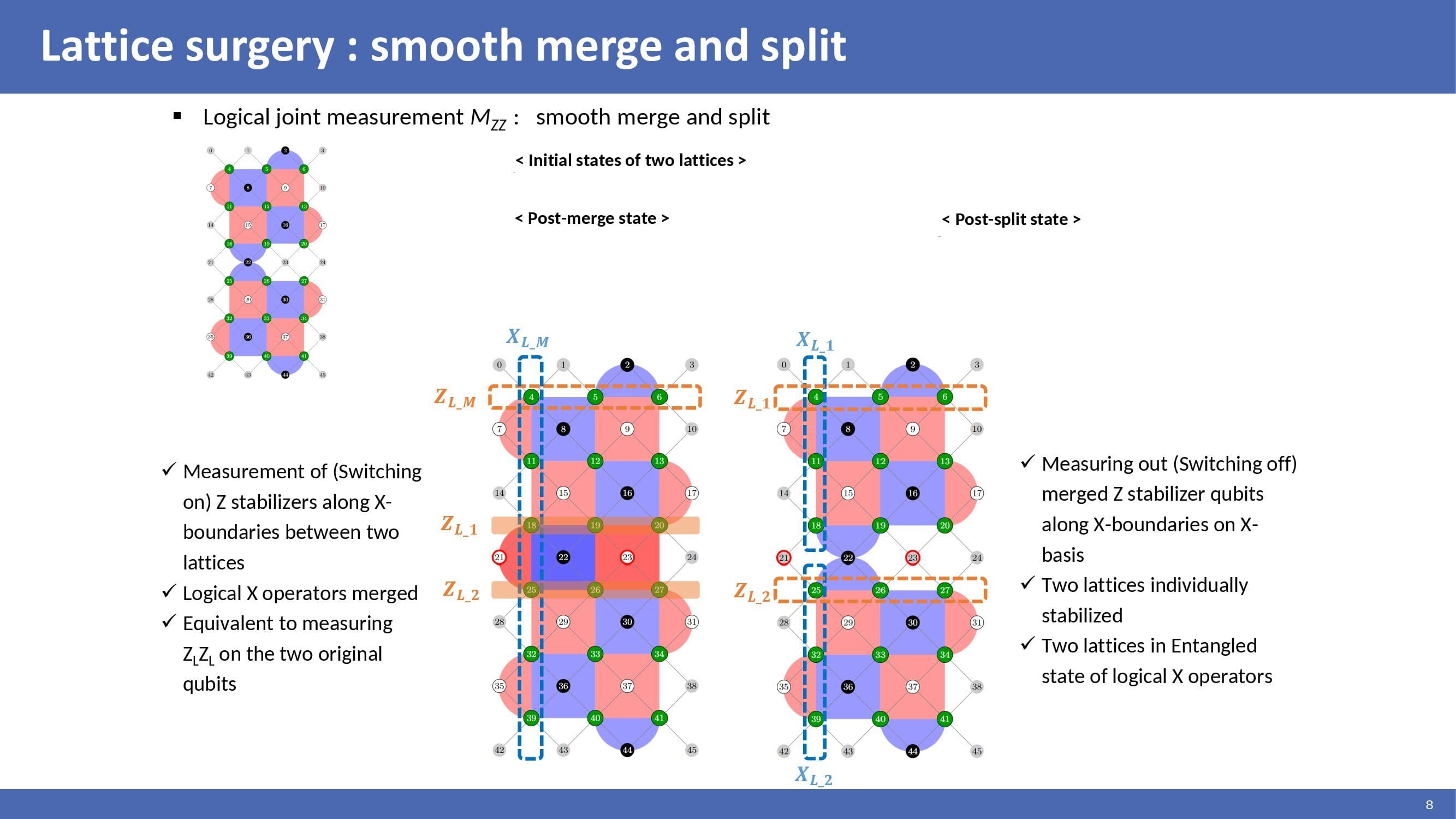Smooth merging is a measurement of Z stabilizer along X-boundaries between two lattices. Logical X operators of two lattices are merged. Smooth merging is equivalent to measuring the logical Z operator of two lattices. Smooth splitting is performed by measuring out merged Z stabilizer qubits along X-boundaries on X-basis. After that, two lattices are individually stabilized. And so, two lattices are in an entangled state of logical X operators.
|
|
ICACT20240330 Slide.06
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
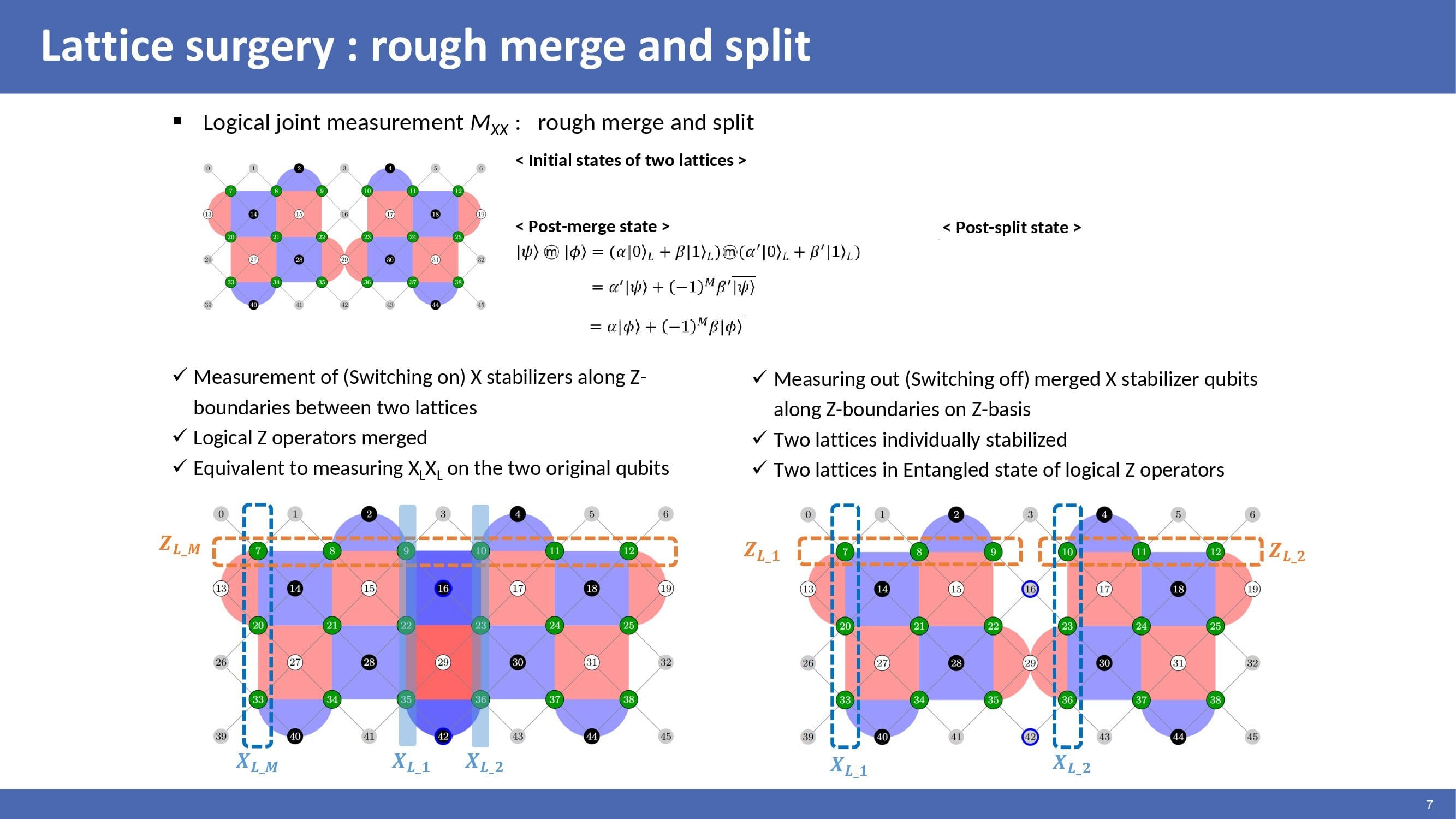Rough merging is a measurement of X stabilizer along Z-boundaries between two lattices. Logical Z operators of two lattices are merged. Rough merging is equivalent to measuring the logical X operator of two lattices. Rough splitting is performed by measuring out merged X stabilizer qubits along Z-boundaries on Z-basis. After that, two lattices are individually stabilized. And so, two lattices are in an entangled state of logical Z operators.
|
|
ICACT20240330 Slide.05
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
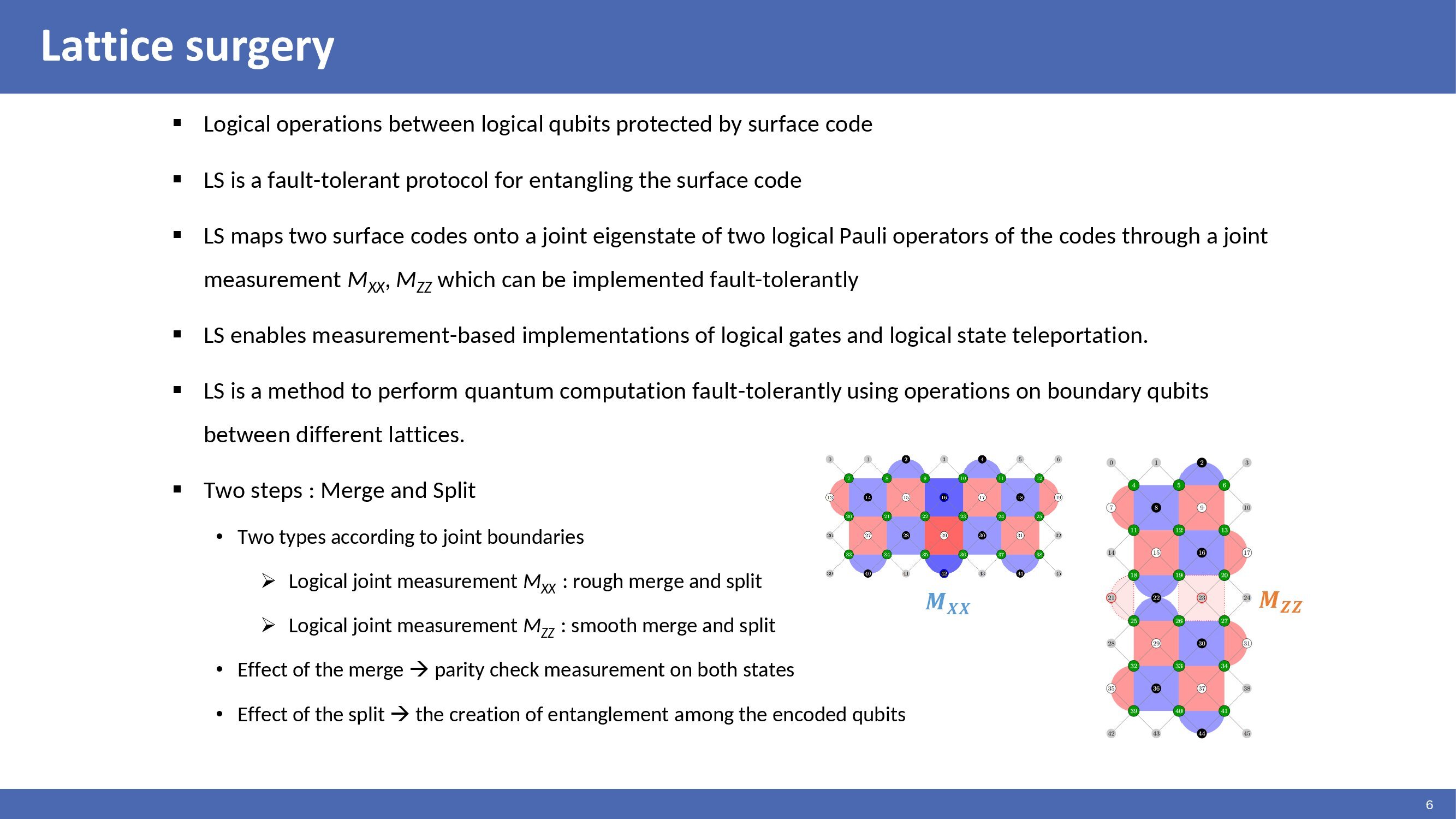Lattice surgery can provide logical operations between logical qubits protected by surface code. Lattice surgery is a fault-tolerant protocol for entangling the surface code. Lattice surgery maps two surface codes onto a joint eigenstate of two logical Pauli operators of the codes through a joint measurement, Mxx or Mzz, which can be implemented fault-tolerantly. Lattice surgery enables measurement-based implementations of logical gates and logical state teleportation. Lattice surgery is a method to perform quantum computation fault-tolerantly using operations on boundary qubits between different lattices. Lattice surgery consists of two steps. There are two types according to joint boundaries. If joint boundaries are rough boundaries, rough merge and split. Otherwise, smooth merge and split. The effect of the merge is a parity check measurement on both states. The effect of the split is the creation of entanglement among the encoded qubits.
|
|
ICACT20240330 Slide.04
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
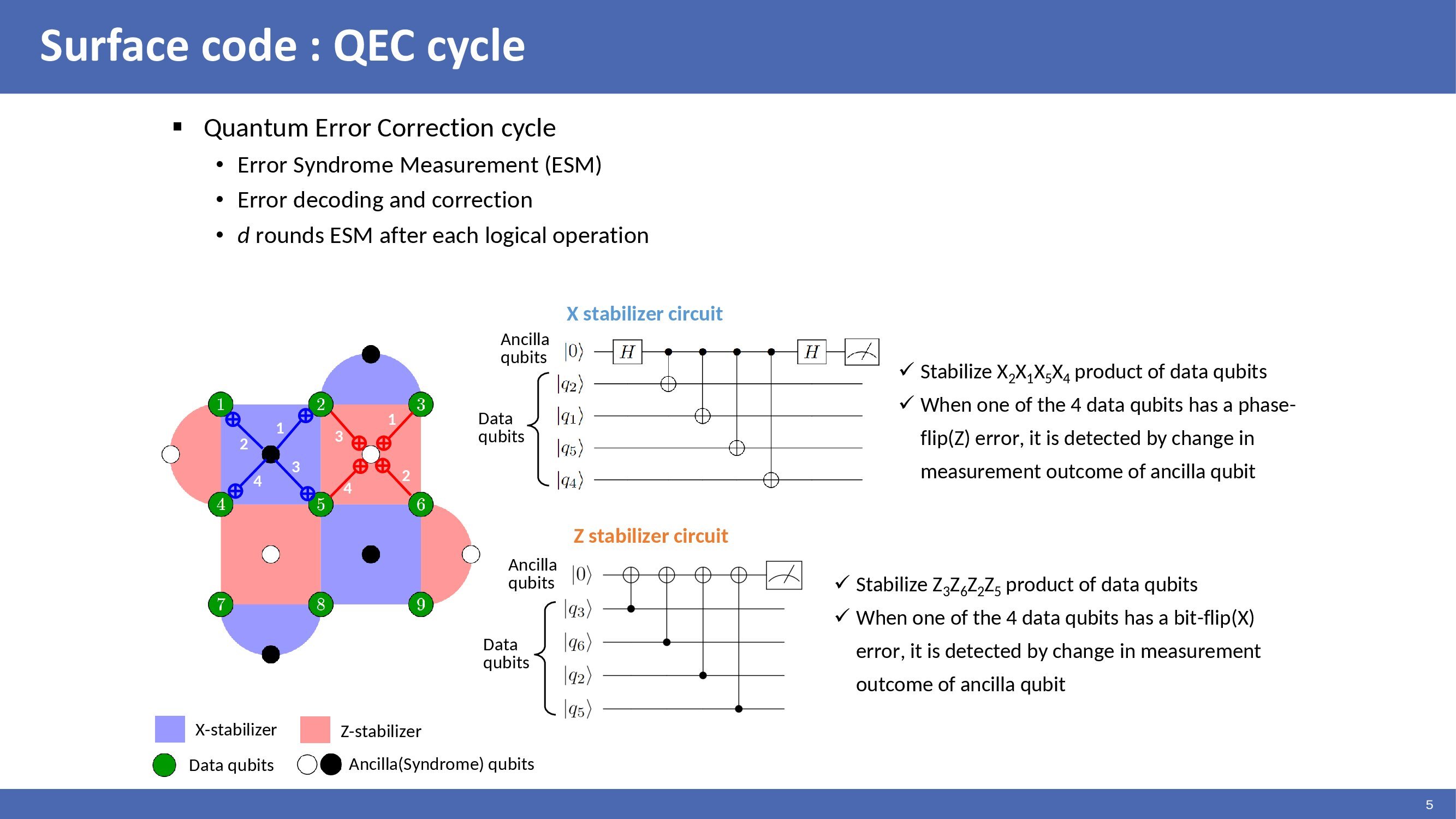Surface code stabilizes data qubit states by performing ESM stabilizer circuits. Data qubit error can be detected by stabilizer measurement outcome. If the stabilizer detects errors, they can be corrected by error decoding and correction procedures. Stabilizer circuits are performed d rounds after each logical operation. X stabilizer stabilizes XXXX product of data qubits. When one of the 4 data qubits has a phase-flip(Z) error, it is detected by a change in the measurement outcome of the ancilla qubit. Z stabilizer stabilizes ZZZZ product of data qubits. When one of the 4 data qubits has a bit-flip(X) error, it is detected by a change in the measurement outcome of the ancilla qubit.
|
|
ICACT20240330 Slide.03
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
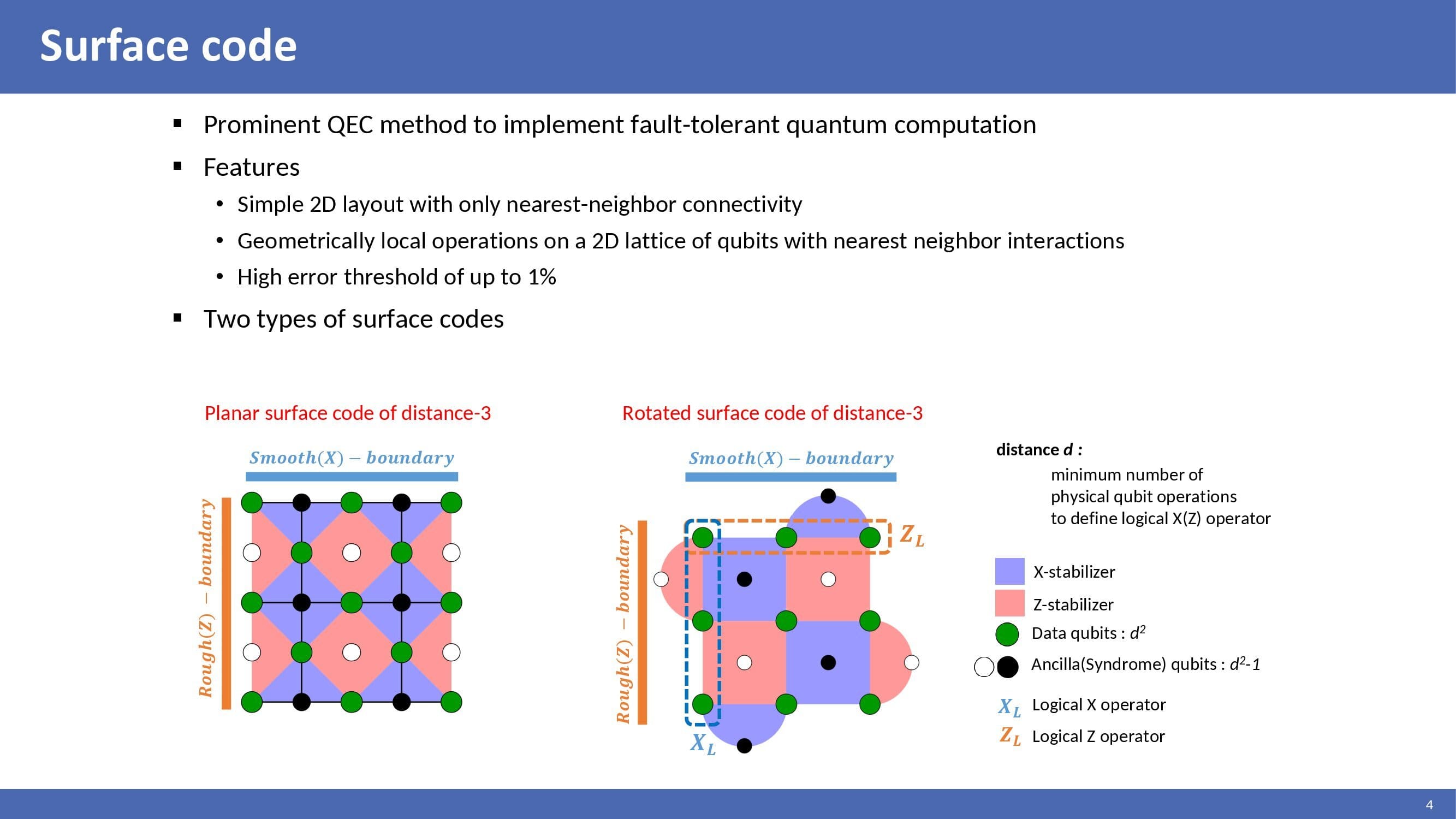Surface code is considered a prominent QEC method to implement fault-tolerant quantum computation. It has the following features. Simple 2D layout with only nearest-neighbor connectivity. Geometrically local operations on a 2D lattice of qubits with nearest neighbor interactions. High error threshold of up to 1%. Generally, there are two types of surface codes: planar and rotated. Rotated surface code is a rotated form of planar surface code. It has the same functionality but can be configured into fewer qubits. Distance is the minimum number of physical qubit operations to define logical X(Z) operator. So distance 3 surface code is the smallest code because it can correct at least single qubit error. In this figure, green circles are physical data qubits, and white or black circles are physical ancilla qubits. The blue and pink plaquettes are X and Z stabilizers, respectively. The figure's top and bottom edges are called smooth or X boundary. The left and the right edges are called rough or Z boundaries. X products connecting X-boundarires are called logical X operators. Z products connecting Z-boundaries are called logical Z operators.
|
|
ICACT20240330 Slide.02
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
We have to consider two issues to implement quantum computer.
First, we need a fault-tolerant quantum computer from quantum devices with noisy qubits and gates. There are many studies on quantum error correction methods, especially topological codes such as surface codes. The lattice surgery model effectively performs logical operations between logical qubits protected by surface code.
Second, we need a universal quantum computer to reap the benefits of quantum computing. Therefore, we must support Clifford and non-Clifford gates. Clifford gates can be efficiently simulated on a classical computer. However, it takes complex work to implement non-Clifford gates locally. In particular, the logical S and T gate can be implemented by lattice surgery-based gate teleportation that requires the magic state. The magic state is injected using a state injection procedure. However, the injected magic state is not fault-tolerant and has low fidelity. Thus, it needs to be distilled by the magic state distillation procedure. Magic state distillation is not easy to implement because it costs many resources and time to obtain a higher-fidelity magic state from multiple lower-fidelity states. Previous studies have proposed several magic state distillation protocols and calculated their costs numerically.
In this work, we have implemented and evaluated magic state distillation processes for |Y>.
|
|
ICACT20240330 Slide.01
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
This is the outline of my presentation. I will start with an overview. Next, I will look at surface code and lattice surgery on surface codes. Then, I will introduce a distillation process for |Y> state and explain two implementation methods for |Y> distillation process. After that, I will show the evaluation results. Lastly, I will summarize.
|
|
ICACT20240330 Slide.00
[Big slide for presentation]
|
Chrome Text-to-Speach Click!! |
 |
Hello, everyone. My name is Youngchul Kim. I am with ETRI in Korea. Today I will be talking about ˇ°Evaluation of |Y> Magic State Distillation Circuit".
|
